几何画板如何验证完全平方公式 几何画板验证完全平方公式的操作流程

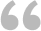
最近不少伙伴咨询几何画板如何验证完全平方公式的操作，今天小编就带来了几何画板验证完全平方公式的操作流程，感兴趣的小伙伴一起来看看吧!　　几何画板验证完全平方公式的操作流程　　新建参数a、b。打开几何画板，执行“数据”——“新建参数”命令，在弹出的对话框输入参数名称a，数值为6，单位选择距离。按照这样的方法新建参数b=2.00cm，并执行“数据”——“计算”命令计算出a+b的值，　　以a+b的值为边长构造正方形。用移动工具选中计算数值，执行“变换”——“标记距离”命令。使用点工具在画板上任意画一点A，选中点执行“变换”——“平移”命令，在弹出的对话框修改角度为0，点击确定，即可得到点B。构造线段AB，双击点A标记为旋转中心，选中线段AB执行“变换”——“旋转”命令，角度为90，点击确定，即可得到点D。选中点D和线段AB构造平行线，同样选中点B和线段AD构造平行线，交点为C，构造线段BC、CD，得到正方形ABCD。　　划分正方形。选中参数a执行“变换”——“标记距离”命令，选中点A执行“变换”——“平移”命令，在弹出的对话框角度为90，点击确定，得到点A’。 选中参数b执行“变换”——“标记距离”命令，选中点C执行“变换”——“平移”命令，在弹出的对话框角度为180，点击确定，得到点C’。过点A’构造AB边的平行线，过点C’构造边AD的平行线，得到交点E。隐藏平行线，构造如下图所示的线段。　　计算将正方形ABCD的面积和分割的四个四边形的面积。正方形ABCD的面积可以表示为：(a+b)*(a+b)，并通过计算得知其值。通过计算可以得出四个小的四边形的面积分别为：ab、ab、a2、b2，通过计算将四个小四边形的面积相加，得到的值应该和正方形ABCD的面积相等，从而可以验证完全平方公式的正确性。　　上文就讲解了几何画板验证完全平方公式的操作流程，希望有需要的朋友都来学习哦。