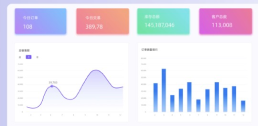
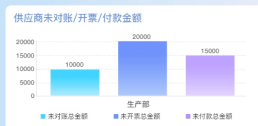
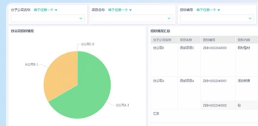
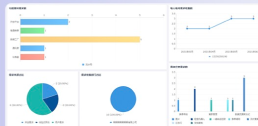
ols回归模型是什么意思

标题：了解OLS回归模型，掌握数据分析利器

在数据分析领域，OLS回归模型是一种常用的统计分析方法。OLS是最小二乘法（Ordinary Least Squares）的缩写，它是一种用来估计线性关系的方法，通过对数据进行拟合来解释自变量和因变量之间的关系。在实际应用中，OLS回归模型被广泛应用于经济学、金融学、社会学、医学等领域，成为数据分析的利器。

OLS回归模型的基本原理是通过最小化残差平方和来确定各个参数的取值，从而得到最佳拟合曲线。在OLS回归模型中，自变量和因变量的线性关系可以用数学方程来表示，通过拟合曲线来预测因变量的取值。OLS回归模型通过对数据的拟合来找出变量之间的关系，帮助我们理解数据的规律和特征。

OLS回归模型的应用范围非常广泛。在经济学领域，OLS回归模型可以用来分析宏观经济变量之间的关系，如GDP和失业率之间的关系、通货膨胀率和利率之间的关系等。在金融学领域，OLS回归模型可以用来研究股票收益率、债券收益率等变量之间的关系，帮助投资者做出理性的投资决策。在社会学领域，OLS回归模型可以用来分析社会变量之间的关系，如教育水平和收入水平之间的关系、人口增长率和经济发展水平之间的关系等。在医学领域，OLS回归模型可以用来分析疾病的发病率和危险因素之间的关系，为疾病预防和控制提供科学依据。

除此之外，OLS回归模型还可以用于预测和控制变量。在预测方面，我们可以利用OLS回归模型来预测因变量的取值，帮助我们做出未来发展的规划和决策。在控制变量方面，OLS回归模型可以帮助我们找出影响因变量的关键因素，从而制定相应的政策和措施来加以控制和改善。

值得注意的是，OLS回归模型也存在一些局限性。首先，OLS回归模型要求自变量和因变量之间存在线性关系，对非线性关系的拟合效果较差；其次，OLS回归模型对异常值敏感，需要对数据进行异常值处理；再次，OLS回归模型要求自变量之间相互独立，排除多重共线性的影响。因此，在应用OLS回归模型时需要注意这些局限性，结合实际问题选择合适的建模方法。

总的来说，OLS回归模型作为一种基本的数据分析方法，具有广泛的应用前景。它能够帮助我们分析数据、理解数据、预测数据，为决策提供科学依据。通过深入了解OLS回归模型的原理和应用，我们可以更好地掌握这一数据分析利器，发挥其在实际工作中的作用，为各行各业提供更精准的数据支持。OLS回归模型的应用是一个长期的学习和探索过程，希望大家能够加强学习，不断提升自己的数据分析能力。